Parmi les théorèmes les plus présents pendant la scolarité, voire après, il y a celui de Pythagore. Il s’agit d’un théorème qui concerne les triangles rectangles. Avez-vous suivi de nombreux cours pour l’apprendre, mais avez-vous du mal à le cerner ? Les explications qui suivent vont vous faciliter les choses.
Le théorème de Pythagore : un triangle pour les triangles rectangles
A lire aussi : Astuces et méthodes efficaces pour résoudre des problèmes mathématiques
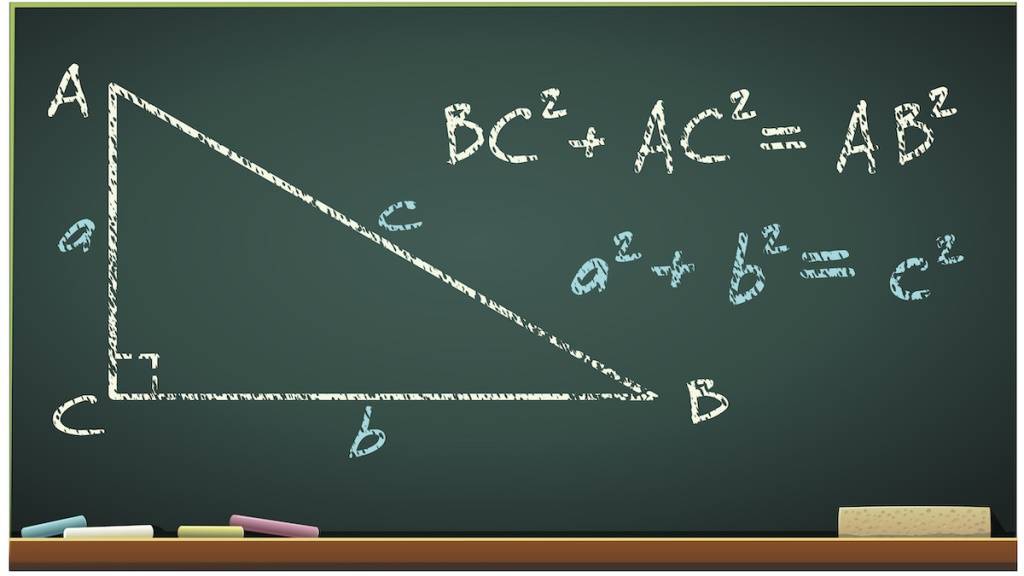
Le théorème de Pythagore est le suivant : « Dans un triangle rectangle, le carré de l’hypoténuse équivaut à la somme des carrés des longueurs des deux autres côtés ». L’hypoténuse en question est le plus grand côté du triangle.
Pour comprendre ce théorème, il faut dessiner un triangle rectangle et ajouter des carrés sur les trois côtés. Il faut ensuite calculer l’aire de chaque carré. L’aire du grand carré doit être égale à la somme de l’aire du petit carré et du carré moyen. Si on a donc un triangle ABC rectangle en C, la formule est : AB² = AC² + BC².
En parallèle : Comment apprendre les maths facilement et sans stress
Le théorème de Pythagore : la réciproque et la contraposée
Le théorème de Pythagore indique aussi que : « Si le carré du plus grand côté du triangle est équivalent à la somme des carrés des deux côtés, alors ce triangle est rectangle ». Il s’agit de la réciproque.
Le théorème de Pythagore parle également de triangle rectangle quand l’angle du sommet est égal à la somme des angles des deux côtés. Dans ce cas, on parle de triangle rectangle isocèle. Cela se produit quand on a un triangle isocèle en A par exemple dont l’angle est de 90° pour le sommet et de 45° de chaque pour les côtés.
Concernant la contraposée, le théorème de Pythagore indique que si le carré de l’hypoténuse (donc le grand côté du triangle) ne correspond pas à la somme des carrés des deux autres côtés, dans ce cas, on ne peut pas parler de triangle rectangle. Cela peut être un triangle isocèle ou encore un triangle équilatéral.
Que peut-on faire avec le théorème de Pythagore ?
Avec le théorème de Pythagore, il devient facile de connaître la longueur de l’hypoténuse d’un triangle rectangle. Il faut juste appliquer la formule en fonction des notations des sommets. À titre illustratif, pour un triangle ABC rectangle en C, on a AB² = AC² + BC². Pour un triangle ABC rectangle en A, on a CB² = CA² + AB².
Avec le théorème de Pythagore, on peut aussi calculer facilement la médiane d’un triangle rectangle. Étant donné que la médiane est une droite qui coupe le triangle rectangle en deux à aires égales, la longueur de celle de l’hypoténuse est donc la moitié de l’hypoténuse. Pour un triangle ABC rectangle en A par exemple, la médiane (AD) = CB/2. Celle-ci est égale aux segments CD et DB.